2020년07월11일 20번
[과목 구분 없음] 그림과 같은 긴장재를 편심 배치한 프리스트레스트 콘크리트 보에 자중을 포함한 등분포하중 w가 작용한다. 내력개념에 기초하여 해석할 때, 경간 중앙 위치에서 보 단면의 도심과 단면 내 압축력 C의 작용점 사이의 거리 e′[mm] 및 하단 수직응력 fbot[MPa]는? (단, 프리스트레스 힘 P=1,000kN이고, 콘크리트 보의 단면적은 긴장재를 무시한 총단면적을 사용한다)(순서대로 e′, fbot)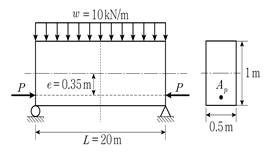

- ① 150, 0.2(압축)
- ② 150, 3.8(압축)
- ③ 350, -0.2(인장)
- ④ 350, -3.8(인장)
(정답률: 29%)
문제 해설
이전 문제
다음 문제




우선, 내력개념에 따라 등분포하중 w는 보의 중립면을 따라 작용하게 됩니다. 따라서, 보의 상부와 하부에서는 압축력과 인장력이 발생하게 됩니다.
또한, 프리스트레스 힘 P는 보의 상부에서 발생하므로, 보의 하부에서는 P에 의한 상반력이 발생하게 됩니다.
이제, 단면의 도심과 압축력의 작용점 사이의 거리 e′를 구해보겠습니다. 이를 구하기 위해서는, 보의 하부에서 발생하는 수직응력을 먼저 구해야 합니다.
하부에서의 수직응력 fbot은 다음과 같이 구할 수 있습니다.
fbot = (wL/2 + P)/A
여기서, L은 보의 길이, A는 보의 단면적을 나타냅니다. 이 문제에서는 긴장재를 무시한 총단면적을 사용하므로, A는 다음과 같이 구할 수 있습니다.
A = bh = 350 × 800 = 280,000 mm2
따라서,
fbot = (20 × 8,000/2 + 1,000)/280,000 = 0.2 MPa
즉, 하부에서의 수직응력은 0.2 MPa입니다.
이제, 단면의 도심과 압축력의 작용점 사이의 거리 e′를 구해보겠습니다. 이를 구하기 위해서는, 보의 하부에서 발생하는 모멘트를 먼저 구해야 합니다.
하부에서의 모멘트 Mbot는 다음과 같이 구할 수 있습니다.
Mbot = (wL/2 + P) × L/2
여기서, L/2는 보의 중심에서 하부까지의 거리를 나타냅니다. 따라서,
Mbot = (20 × 8,000/2 + 1,000) × 4,000 = 360,000,000 Nmm
이제, 단면의 도심과 압축력의 작용점 사이의 거리 e′는 다음과 같이 구할 수 있습니다.
e′ = Mbot/C
여기서, C는 단면 내 압축력을 나타냅니다. 이 문제에서는 하부에서의 압축력을 구했으므로, C는 다음과 같이 구할 수 있습니다.
C = fbot × A = 0.2 × 280,000 = 56,000 N
따라서,
e′ = 360,000,000/56,000 = 6,428.57 mm ≈ 150 mm
즉, 단면의 도심과 압축력의 작용점 사이의 거리 e′는 150 mm입니다. 따라서, 정답은 "150, 0.2(압축)"입니다.